Der Variationskoeffizient (CV) ist ein unverzichtbares Werkzeug in der Datenanalyse, insbesondere wenn es darum geht, die Variabilität unterschiedlicher Datensätze miteinander zu vergleichen. Seine Stärke liegt darin, dass er die Streuung von Daten standardisiert, selbst wenn diese in unterschiedlichen Einheiten vorliegen. Dieser Artikel beleuchtet die Bedeutung des CV, seine Berechnung in gängigen Tabellenkalkulationsprogrammen und seine vielfältigen Anwendungsbereiche.
Was ist der Variationskoeffizient?
Der Variationskoeffizient misst die Streuung von Datenpunkten relativ zu ihrem Mittelwert. Er ermöglicht den Vergleich der Variabilität von zwei oder mehr Datensätzen, die unterschiedliche Einheiten oder Mittelwerte aufweisen können. Ein niedrigerer CV deutet darauf hin, dass die Datenpunkte näher am Mittelwert liegen, was auf eine geringere Variabilität schließen lässt. Ein höherer CV hingegen zeigt eine größere Streuung der Datenpunkte um den Mittelwert und somit eine höhere Variabilität an.
Diese Kennzahl ist besonders in der Finanz- und Investmentbranche von großer Bedeutung. Die Volatilität von Preisen kann direkte Auswirkungen auf potenzielle Renditen haben. Ein niedriger CV signalisiert hier ein geringeres Risiko im Verhältnis zur erwarteten Rendite, was für fundierte Anlageentscheidungen entscheidend ist.
Berechnung des Variationskoeffizienten in Excel und Google Sheets
Der Variationskoeffizient wird berechnet, indem die Standardabweichung eines Datensatzes durch dessen Mittelwert geteilt und das Ergebnis mit 100 multipliziert wird, um es als Prozentsatz auszudrücken. Die Formel lautet:
CV = (Standardabweichung / Mittelwert) * 100
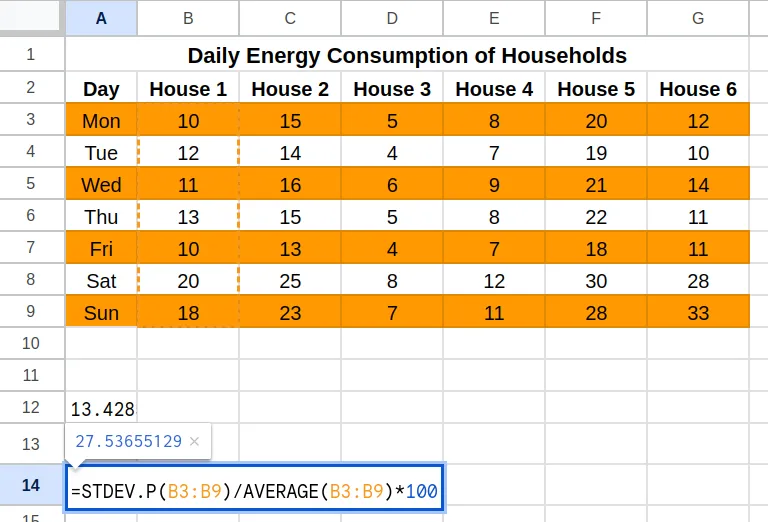
Da weder Microsoft Excel noch Google Sheets eine direkte Funktion zur Berechnung des CV bieten, ist ein dreistufiger Prozess erforderlich. Anhand eines Beispieldatensatzes, der den durchschnittlichen Stromverbrauch (in kWh) von Häusern über verschiedene Wochentage hinweg zeigt, lässt sich die Berechnung nachvollziehen:
- Berechnung der Standardabweichung: In einer leeren Zelle wird die Formel
=STABW.N(B3:B9)(oder eine ähnliche Funktion je nach Excel-Version und Datensatz) eingegeben, um die Standardabweichung für das jeweilige Haus zu ermitteln. Dieser Schritt wird für alle Datensätze wiederholt. - Berechnung des Mittelwerts: In einer weiteren leeren Zelle wird die Formel
=MITTELWERT(B3:B9)verwendet, um den Durchschnittswert für jeden Datensatz zu berechnen. - Berechnung des Variationskoeffizienten: Abschließend wird in einer Zelle die Formel
=(Standardabweicher-Zelle / Mittelwert-Zelle) * 100eingegeben. Alternativ kann die Formel direkt mit den Zellbezügen der vorherigen Schritte angewendet werden, z. B.=DIVIDE(A13,A12)*100, wobei A13 die Zelle mit der Standardabweichung und A12 die Zelle mit dem Mittelwert ist.
 Berechnung des Variationskoeffizienten in Excel und Google Sheets
Berechnung des Variationskoeffizienten in Excel und Google Sheets
Praktische Überlegungen bei der CV-Berechnung
Bei der Anwendung des Variationskoeffizienten sind einige Punkte zu beachten:
- Mittelwerte nahe Null: Wenn der Mittelwert eines Datensatzes null oder nahe null ist, kann der CV irreführend werden. In solchen Fällen sind alternative Maße wie die Standardabweichung oder der Interquartilsabstand möglicherweise besser geeignet.
- Datenverteilung: Der CV ist am aussagekräftigsten bei normalverteilten Daten. Schiefe Verteilungen oder Ausreißer können den CV verzerren. Es ist daher ratsam, die Datenverteilung zu prüfen, bevor man sich ausschließlich auf den CV verlässt.
- Skalenniveaus der Daten: Der CV eignet sich am besten für Verhältnisskalen (z. B. Preise, Gewichte). Bei Intervallskalen (z. B. Temperaturen) kann die Anwendung zu Fehlinterpretationen führen.
Reale Anwendungen des Variationskoeffizienten
Datenanalysten in verschiedensten Branchen nutzen den CV, um ihre Daten besser zu verstehen.
Finanzen und Risikobewertung
Im Finanzwesen vergleichen Investoren die CV-Werte von Vermögenswerten, um Anlageentscheidungen zu treffen. Ein niedrigerer CV deutet auf ein besseres Verhältnis von Rendite zu Risiko hin.
Qualitätskontrolle in der Fertigung
In der Produktion hilft der CV, die Konsistenz von Produkteigenschaften über verschiedene Chargen hinweg sicherzustellen. Ein niedriger CV ist ein Indikator für geringe Schwankungen und somit für hohe Produktqualität.
Wetteranalyse
Meteorologen verwenden den CV zur Untersuchung der Beständigkeit von Wettermustern, wie z. B. Niederschlagsschwankungen. Dies trägt zur Verbesserung von Wettervorhersagen bei.
Biologie und Medizin
In der Forschung wird der CV zur Bewertung der Wiederholbarkeit und Zuverlässigkeit von experimentellen Ergebnissen eingesetzt, was für die wissenschaftliche Validität unerlässlich ist.
Fazit
Der Variationskoeffizient ist ein mächtiges Instrument zum Vergleich der relativen Variabilität von Datensätzen. Die einfache Berechnung in Excel oder Google Sheets liefert wertvolle Einblicke in die Konsistenz von Datenpunkten und findet breite Anwendung in der Finanzanalyse, Qualitätskontrolle und wissenschaftlichen Forschung. Durch die Anwendung dieses Schritt-für-Schritt-Leitfadens können Sie den CV effektiv in Ihrer Datenanalyse nutzen, um fundiertere Entscheidungen auf Basis der Datenvariabilität zu treffen.
